Link state protocols like OSPF and IS-IS use the Shortest Path First (SPF) algorithm developed by Edsger Dijkstra. Edsger was a Dutch computer scientist, programmer, software engineer, mathematician, and science essayist. He wanted to solve the problem of finding the shortest distance between two cities such as Rotterdam and Groningen. The solution came to him when sitting in a café and the rest is history. SPF is used in many applications, such as GPS, but also in routing protocols, which I’ll cover today.
To explain SPF, I’ll be working with the following topology:
Note that SPF only works with a weighted graph where we have positive weights. I’m using symmetrical costs, although you could have different costs in each direction. Before running SPF, we need to build our Link State Database (LSDB) and I’ll be using IS-IS in my lab for this purpose. Based on the topology above, we can build a table showing the cost between the nodes:
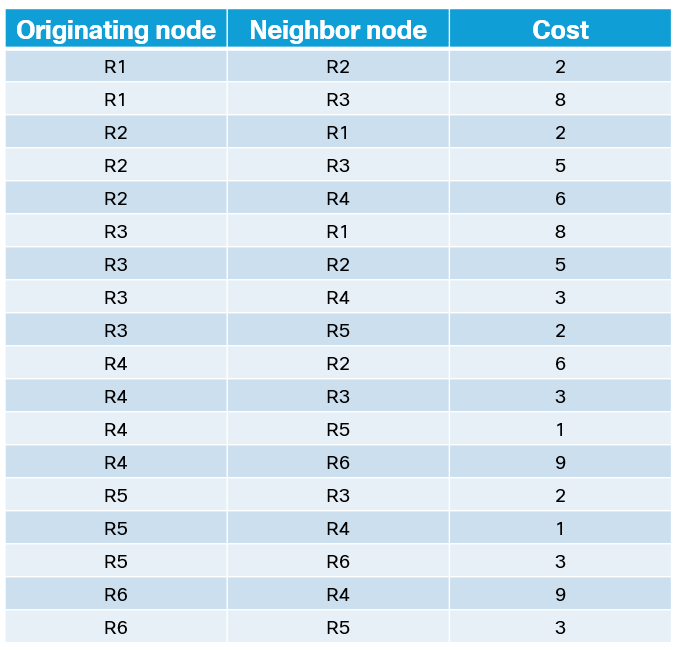
This triplet of information consists of originating node, neighbor node, and cost. It can also be represented as [R1, R2, 2], [R1, R3, 8], [R2, R1, 2], [R2, R3, 5], [R2, R4, 6], [R3, R1, 8], [R3, R2, 5], [R3, R4, 3], [R3, R5, 2], [R4, R2, 6], [R4, R3, 3], [R4, R5, 1], [R4, R6, 9], [R5, R3, 2], [R5, R4, 1], [R5, R6, 3], [R6, R4, 9], [R6, R5, 3].
To be able to perform SPF, we need data structures, call them sets or lists:
- TENT – Tentative, these are candidate best paths. If determined to be the best path, they are moved to the PATH list.
- PATH – These are the determined best paths. There is no shorter path available.
The node performing SPF is often referred to as self or root, because it’s the root of the tree we’re calculating. This node will insert itself to the PATH list with a cost of 0 (to itself) with a next-hop of itself. The triplet of information in these lists will consist of {node we’re trying to reach, total cost from calculating node, next-hop to reach node}. Initially, this would be {R1, 0, R1}.
At a high level, the algorithm works like this:
- 1. Build the LSDB
- 2. Initialize TENT and PATH databases
- 3. Add root to PATH {root, 0, root}
- 4. Add all nodes adjacent to root to TENT
- 5. Move lowest-cost node from TENT to PATH (pick randomly if equal cost)
- 6. Add all adjacent nodes of chosen node to TENT (unless node already in PATH)
- 7. Calculate cost from root to each node in TENT (if node already in TENT with higher cost, replace it with lower-cost entry)
- 8. Move lowest-cost node from TENT to PATH
- 9. Delete higher-cost entries for node in TENT
- 10. If entries remain in TENT, go to step 6
- 11. If no entries remain in TENT, stop
Visually, it would look like this:
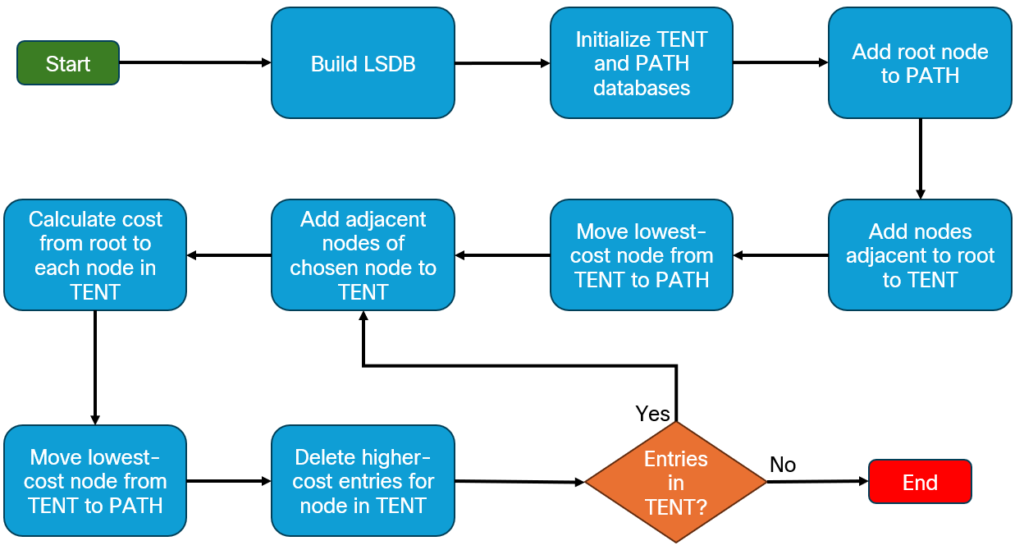
With an understanding of the algorithm, let’s perform the SPF calculation from R1’s perspective. Step 1 and 2 have already been performed so we start at step 3.
Step3 – R1 inserts itself into PATH and there is nothing in TENT yet:
PATH – {R1, 0, R1}
TENT – {}
Step 4 – Now the nodes adjacent to R1 are added to TENT:
PATH – {R1, 0, R1}
TENT – {R2, 2, R1}, {R3, 8, R1}
Step 5 – R2 is the lowest-cost node so it’s moved from TENT to PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}
TENT – {R3, 8, R1}
Step 6 – Next, adjacent nodes of R2 are added to TENT:
PATH – {R1, 0, R1}, {R2, 2, R1}
TENT – {R3, 8, R1}, {R3, 5, R2}, {R4, 6, R2}
Note that we don’t add R1 to TENT even though R2 is adjacent to R1 because R1 is already in PATH.
Step 7 – Currently the costs in TENT where R2 is next-hop don’t have the full cost, we need to add the cost from R1 to R2 to the entries where R2 is the next-hop. We then have the following lists:
PATH – {R1, 0, R1}, {R2, 2, R1}
TENT – {R3, 8, R1}, {R3, 7, R2}, {R4, 8, R2}
Step 8 – The lowest-cost entry is now R3 with a cost of 7 and a next-hop of R2. We move it to PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}
TENT – {R3, 8, R1}, {R4, 8, R2}
Step 9 – Remove R3 entry from TENT because it is already in PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}
TENT – {R4, 8, R2}
Step 10 – There are still entries in TENT so we go to step 6, which is to add adjacent nodes of R3 to TENT:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}
TENT – {R4, 8, R2}, {R4, 3, R2}, {R5, 2, R2}
Note that we didn’t add R1 and R2 because they are already in PATH. Now we need to add the cost of R1 to R3 where R2 is the next-hop:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}
TENT – {R4, 8, R2}, {R4, 10, R2}, {R5, 9, R2}
The lowest-cost entry is now R4 so we add it to PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}
TENT – {R4, 10, R2}, {R5, 9, R2}
The R4 entry is removed because it’s already in PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}
TENT – {R5, 9, R2}
TENT isn’t empty yet so adjacent nodes of R4 are added to TENT:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}
TENT – {R5, 9, R2}, {R5, 1, R2}, {R6, 9, R2}
Note that R2 and R3 are already in PATH so we don’t add them. We need to add the cost of R1 to R4 where R2 is next-hop:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}
TENT – {R5, 10, R3}, {R5, 9, R2}, {R6, 17, R2}
The lowest-cost entry is now R5 so we add it to PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}
TENT – {R5, 10, R3}, {R6, 17, R2}
The R5 entry is removed because it’s already in PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}
TENT – {R6, 17, R2}
TENT isn’t empty yet so adjacent nodes of R5 are added to TENT:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}
TENT – {R6, 17, R2}, {R6, 3, R2}
Note that R4 and R4 are already in PATH so we don’t add them. We need to add the cost of R1 to R5 where R2 is next-hop:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}
TENT – {R6, 17, R2}, {R6, 12, R2}
The lowest-cost entry is now R6 so we add it to PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}, {R6, 12, R2}
TENT – {R6, 17, R2}
The R6 entry is removed because it’s already in PATH:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}, {R6, 12, R2}
TENT –
As TENT is now empty, SPF has been completed. Note that from R1’s perspective, all nodes have a shortest path via R2. To verify this, and grab some SPF debugs, we’ll implement this in the lab.
The following debugs are enabled on R1:
R1#debug isis spf-events IS-IS SPF events debugging is on for IPv4 unicast topology base R1#debug isis spf-statistics IS-IS SPF Timing and Statistics Data debugging is on for IPv4 unicast topology base R1#debug isis spf-triggers IS-IS SPF triggering events debugging is on for IPv4 unicast topology base
R1 has all the LSPs in the LSDB:
R1#show isis data IS-IS Level-2 Link State Database: LSPID LSP Seq Num LSP Checksum LSP Holdtime/Rcvd ATT/P/OL R1.00-00 * 0x00000005 0xE08B 1195/* 0/0/0 R2.00-00 0x0000000A 0x1CF1 1194/1199 0/0/0 R3.00-00 0x0000000C 0xEDB3 1194/1198 0/0/0 R4.00-00 0x0000000A 0x1960 1194/1100 0/0/0 R5.00-00 0x00000008 0xF4DF 1194/1148 0/0/0 R6.00-00 0x00000007 0x28ED 1194/1177 0/0/0
When we did our manual SPF, we ended up with a PATH that looked like this:
PATH – {R1, 0, R1}, {R2, 2, R1}, {R3, 7, R2}, {R4, 8, R2}, {R5, 9, R2}, {R6, 12, R2}
Let’s now compare that to the routing table, looking for loopbacks of the other routers where the last octet matches the router’s number:
R1#show ip route isis | i 192
192.0.2.0/32 is subnetted, 6 subnets
i L2 192.0.2.2 [115/2] via 172.16.0.2, 00:02:55, GigabitEthernet0/0
i L2 192.0.2.3 [115/7] via 172.16.0.2, 00:02:55, GigabitEthernet0/0
i L2 192.0.2.4 [115/8] via 172.16.0.2, 00:02:55, GigabitEthernet0/0
i L2 192.0.2.5 [115/9] via 172.16.0.2, 00:02:55, GigabitEthernet0/0
i L2 192.0.2.6 [115/12] via 172.16.0.2, 00:02:55, GigabitEthernet0/0
Looks like we were spot on!
Now let’s look at the debugs. R1 is moved into PATH:
ISIS-SPF: Move 0100.0000.0001.00-00 to PATHS, metric 0
Now let’s add neighbors of R1 to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0001.00-00)(7), lsptype:0 ISIS-SPF: considering adj to 0100.0000.0002 (GigabitEthernet0/0) metric 2, level 2, circuit 3, adj 2 ISIS-SPF: (accepted) ISIS-Spf: Add 0100.0000.0002.00-00 to TENT, metric 2 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: neighbor_lsp:0xD2C00B0, lsp_index:2 ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: considering adj to 0100.0000.0003 (GigabitEthernet0/1) metric 8, level 2, circuit 3, adj 2 ISIS-SPF: (accepted) ISIS-Spf: Add 0100.0000.0003.00-00 to TENT, metric 8 ISIS-Spf: Next hop 0100.0000.0003 (GigabitEthernet0/1)
R2 has the lower metric to it’s added to PATH:
ISIS-SPF: Move 0100.0000.0002.00-00 to PATHS, metric 2 ISIS-SPF: Remove the node from the TENT list lsp(0100.0000.0002.00-00)(1):0xD2BF3E0
Now let’s add R2’s neighbors to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0002.00-00)(1), lsptype:0 ISIS-SPF: Replacing 0100.0000.0003.00-00 from TENT, old metric 8, new metric 7 ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-Spf: Add 0100.0000.0003.00-00 to TENT, metric 7 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-Spf: Add 0100.0000.0004.00-00 to TENT, metric 8 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: neighbor_lsp:0xD2D53F0, lsp_index:7 Failed to add neighbor lsp to the tent list, link_is_p2p:1
Now R3 is moved to PATH:
ISIS-SPF: Move 0100.0000.0002.00-00 to PATHS, metric 2 ISIS-SPF: Remove the node from the TENT list lsp(0100.0000.0002.00-00)(1):0xD2BF3E0
Add R3’s neighbors to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0003.00-00)(2), lsptype:0 ISIS-SPF: lsptype:0, current_lsp(0100.0000.0003.00-00)(2) current_lsp:0xD2C00B0, lsp_fragment:0xD2C00B0 calling isis_walk_lsp ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-Spf: Add 0100.0000.0005.00-00 to TENT, metric 9 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: neighbor_lsp:0xD2BFC78, lsp_index:5 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: neighbor_lsp:0xD2BF3E0, lsp_index:1 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: neighbor_lsp:0xD2D53F0, lsp_index:7 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1
Note the “Failed to add neighbor lsp to the tent list” to messages. I’m not exactly sure what they mean, but I think it has to do with not being able to add to TENT because there is already a lower metric entry, so it gets ignored.
Now move R4 to PATH:
ISIS-SPF: Move 0100.0000.0004.00-00 to PATHS, metric 8 ISIS-SPF: Remove the node from the TENT list lsp(0100.0000.0004.00-00)(5):0xD2BFC78
Add R4’s neighbors to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0004.00-00)(5), lsptype:0 ISIS-SPF: lsptype:0, current_lsp(0100.0000.0004.00-00)(5) current_lsp:0xD2BFC78, lsp_fragment:0xD2BFC78 calling isis_walk_lsp ISIS-SPF: neighbor_lsp:0x111487F0, lsp_index:4 ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-Spf: Add 0100.0000.0005.00-00 to TENT, metric 9 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-Spf: Add 0100.0000.0006.00-00 to TENT, metric 17 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: neighbor_lsp:0xD2C00B0, lsp_index:2 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: neighbor_lsp:0xD2BF3E0, lsp_index:1 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1
Now move R5 to PATH:
ISIS-SPF: Move 0100.0000.0005.00-00 to PATHS, metric 9 ISIS-SPF: Remove the node from the TENT list lsp(0100.0000.0005.00-00)(4):0x111487F0
Add R5’s neighbors to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0005.00-00)(4), lsptype:0 ISIS-SPF: lsptype:0, current_lsp(0100.0000.0005.00-00)(4) current_lsp:0x111487F0, lsp_fragment:0x111487F0 calling isis_walk_lsp ISIS-SPF: neighbor_lsp:0x111483B8, lsp_index:3 ISIS-SPF: Replacing 0100.0000.0006.00-00 from TENT, old metric 17, new metric 12 ISIS-SPF: Added neighbor lsp to the tent list, link_is_p2p:1 ISIS-Spf: Add 0100.0000.0006.00-00 to TENT, metric 12 ISIS-Spf: Next hop 0100.0000.0002 (GigabitEthernet0/0) ISIS-SPF: neighbor_lsp:0xD2BFC78, lsp_index:5 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: neighbor_lsp:0xD2C00B0, lsp_index:2 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1
Notice that we found a better path to R6, with a metric of 12 as opposed to 17. Now move R6 to PATH:
ISIS-SPF: Move 0100.0000.0006.00-00 to PATHS, metric 12 ISIS-SPF: Remove the node from the TENT list lsp(0100.0000.0006.00-00)(3):0x111483B8
Add R6’s neighbors to TENT:
ISIS-SPF: Attempt to add each adj of the node to tent via add lsp routes, lsp(0100.0000.0006.00-00)(3), lsptype:0 ISIS-SPF: lsptype:0, current_lsp(0100.0000.0006.00-00)(3) current_lsp:0x111483B8, lsp_fragment:0x111483B8 calling isis_walk_lsp ISIS-SPF: neighbor_lsp:0x111487F0, lsp_index:4 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1 ISIS-SPF: neighbor_lsp:0xD2BFC78, lsp_index:5 ISIS-SPF: Failed to add neighbor lsp to the tent list, link_is_p2p:1
There is nothing more to add, so SPF completes:
ISIS-Stats: SPF only compute time 0.040 ISIS-Stats: IPv4 RIB only compute time 0.004 ISIS-Stats: Complete L2 SPT, ISIS-Stats: Compute time 0.044/0.044, 6/0 nodes, 9/0 links, 0 suspends
We can confirm the topology with show isis topology:
R1#show isis topology IS-IS TID 0 paths to level-2 routers System Id Metric Next-Hop Interface SNPA R1 -- R2 2 R2 Gi0/0 5254.0042.59e4 R3 7 R2 Gi0/0 5254.0042.59e4 R4 8 R2 Gi0/0 5254.0042.59e4 R5 9 R2 Gi0/0 5254.0042.59e4 R6 12 R2 Gi0/0 5254.0042.59e4
With SPF being complete, the topology from R1’s perspective now looks like this:
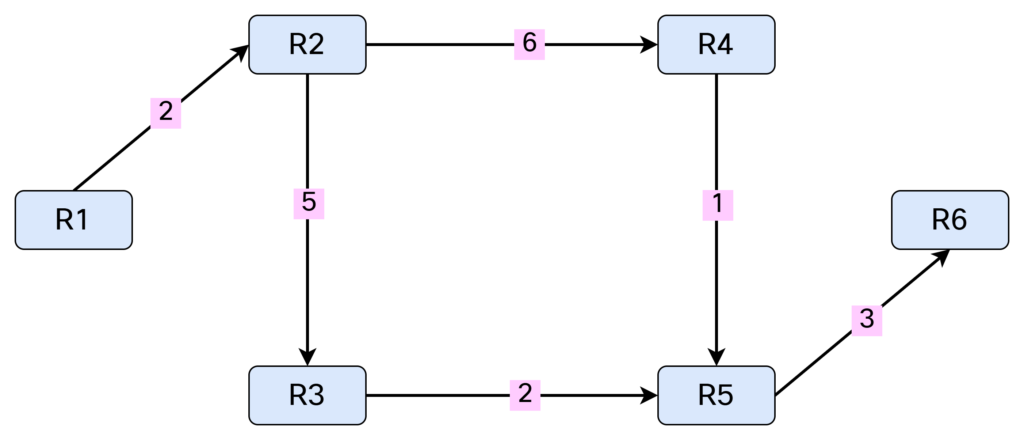
Finally, let’s confirm with a traceroute that packets flow as we expect them to. Let’s start with R2:
R1#traceroute 192.0.2.2 Type escape sequence to abort. Tracing the route to 192.0.2.2 VRF info: (vrf in name/id, vrf out name/id) 1 R1-R2 (172.16.0.2) 4 msec * 4 msec
One hop as expected. R3 should be reachable via R2:
R1#traceroute 192.0.2.3 Type escape sequence to abort. Tracing the route to 192.0.2.3 VRF info: (vrf in name/id, vrf out name/id) 1 R1-R2 (172.16.0.2) 4 msec 4 msec 5 msec 2 R2-R3 (172.16.0.10) 5 msec * 6 msec
R4 should also be reachable via R2:
R1#traceroute 192.0.2.4 Type escape sequence to abort. Tracing the route to 192.0.2.4 VRF info: (vrf in name/id, vrf out name/id) 1 R1-R2 (172.16.0.2) 3 msec 3 msec 3 msec 2 R2-R4 (172.16.0.14) 5 msec * 5 msec
R5 should be reachable via R2 and R3 (or R2 and R4):
R1#traceroute 192.0.2.5 Type escape sequence to abort. Tracing the route to 192.0.2.5 VRF info: (vrf in name/id, vrf out name/id) 1 R1-R2 (172.16.0.2) 4 msec 6 msec 4 msec 2 R2-R3 (172.16.0.10) 6 msec 6 msec 5 msec 3 R3-R5 (172.16.0.22) 7 msec * 7 msec
R6 should be reachable via R2, R3, and R5 (or R2, R4, and R5):
R1#traceroute 192.0.2.6 Type escape sequence to abort. Tracing the route to 192.0.2.6 VRF info: (vrf in name/id, vrf out name/id) 1 R1-R2 (172.16.0.2) 4 msec 5 msec 4 msec 2 R2-R4 (172.16.0.14) 6 msec 5 msec 5 msec 3 R4-R5 (172.16.0.26) 6 msec 5 msec 9 msec 4 R5-R6 (172.16.0.34) 10 msec * 7 msec
In this post we learned about how Dijkstra’s algorithm is used to find the shortest path. The calculation is always started from root, adding itself with a cost of 0. From there, the algorithm looks at the neighbors of the root and adds them to TENT. The best entry is then moved to PATH. From there, new entries are added to TENT and the cycle continues until the TENT is empty. Keep in mind that Dijkstra’s algorithm works for graphs with positive weights.